Vgrid DGGS key features¶

You can try out Vgrid DGGS by using the cloud-computing platforms below without having to install anything on your computer. Full Vgrid DGGS documentation is available at vgrid document.

To work with Vgrid DGGS directly in GeoPandas and Pandas, use the vgridpandas package. Full Vgridpandas DGGS documentation is available at vgridpandas document.

To work with Vgrid DGGS in QGIS, install the Vgrid Plugin.

To visualize DGGS in Maplibre GL JS, try the vgrid-maplibre library.

For an interactive demo, visit the Vgrid Homepage.

References:¶

• h3-py by Uber.
• s2sphere by Sidewalk Labs.
• a5-py by Felix Palmer and Thang Quach.
• rhealpixdggs-py by Manaaki Whenua – Landcare Research.
• open-eaggr by Riskaware.
• EASE-DGGS by GEMS-UMN.
• pydggal by Jerome St-Louis from Ecere.
• DGGRID by Kevin Sahr.
• dggrid4py by Alex Kmoch.
• QTM by Thang Quach, with reference to QTM by Paulo Raposo.
• Lat Lon Tools QGIS Plugin by Calvin Hamilton.
• gars-field by Corteva Agriscience.
• Tilecode & Quadkey by Thang Quach, utilizing mercantile by Mapbox.
• antimeridian by gadomski.
• The DGGS Inspect feature in Vgrid is inspired by Area and shape distortions in open-source discrete global grid systems by Alex Kmoch et al. (2022) (resources).
• The Vgrid Document is inspired by leafmap developed by Qiusheng Wu from Open Geospatial Solutions.

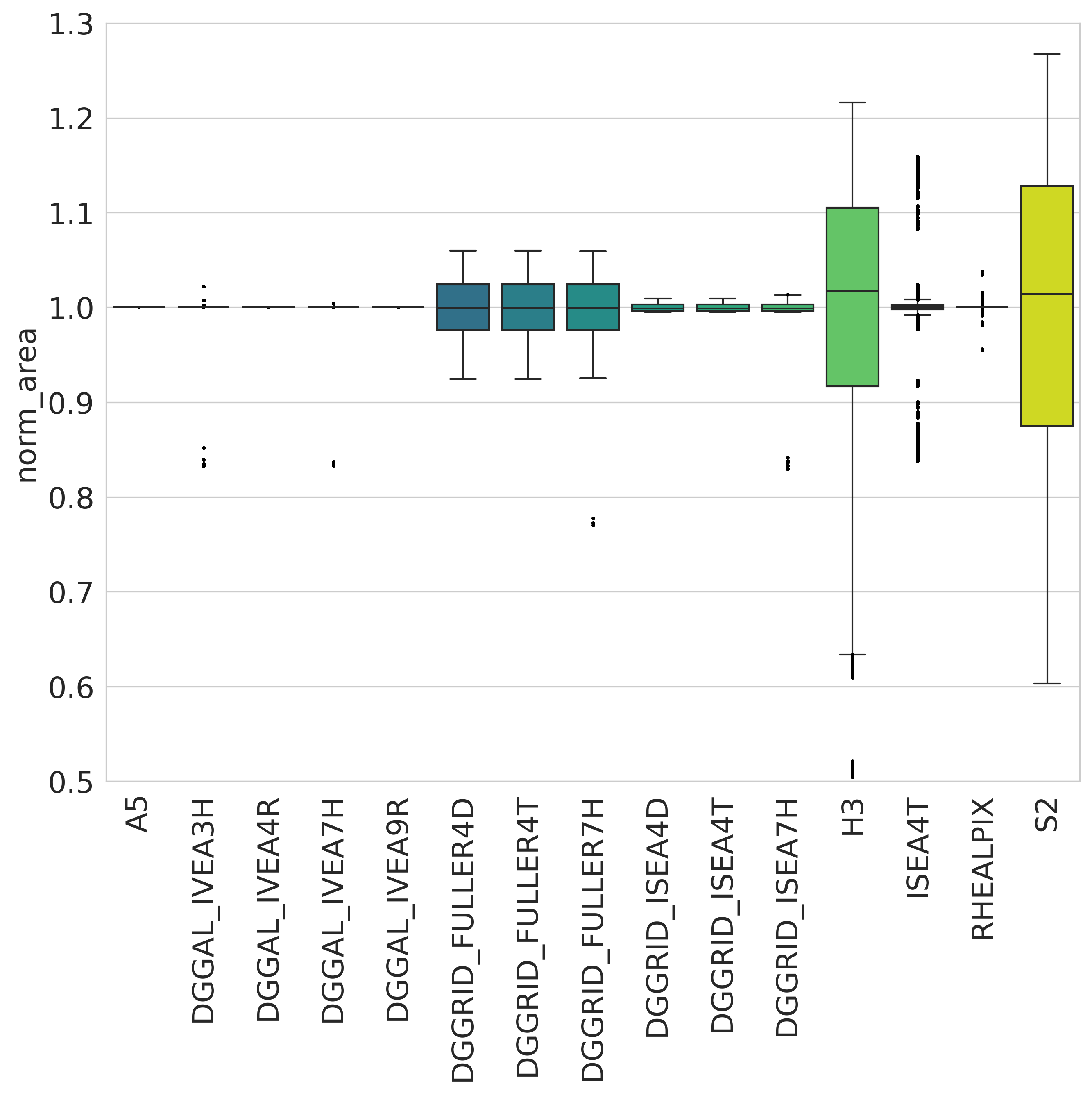
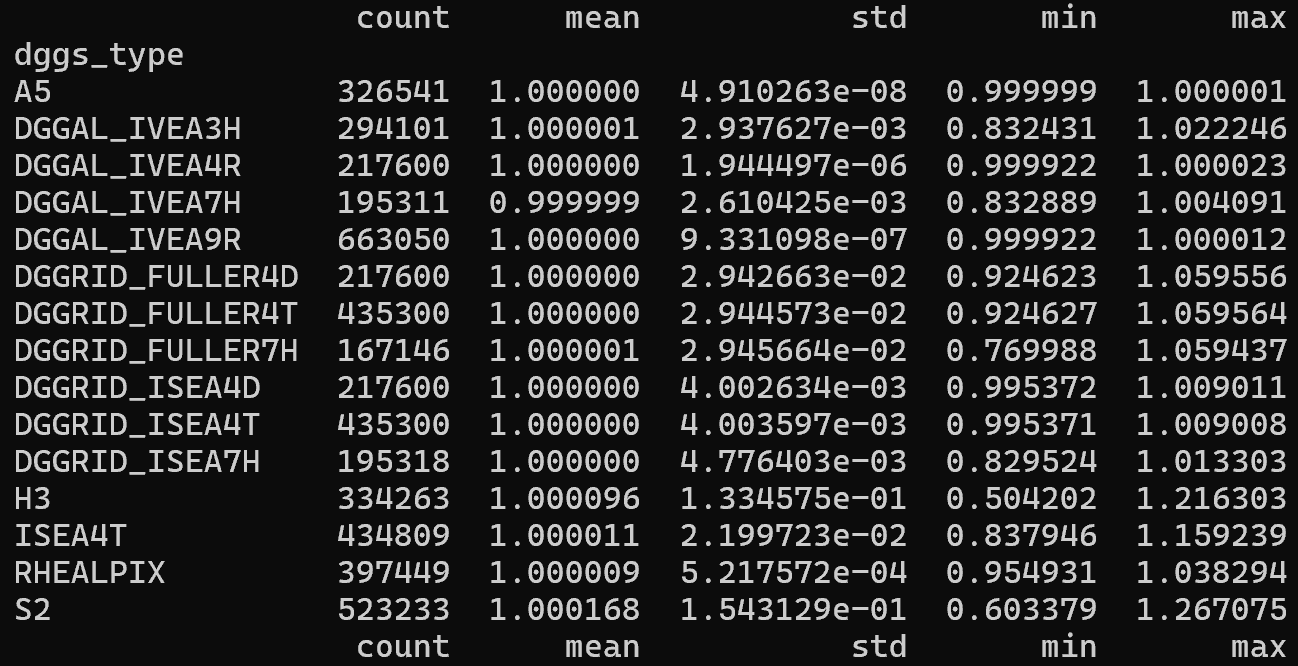
Area distortion over normalized areas of popular geodesic DGGS¶

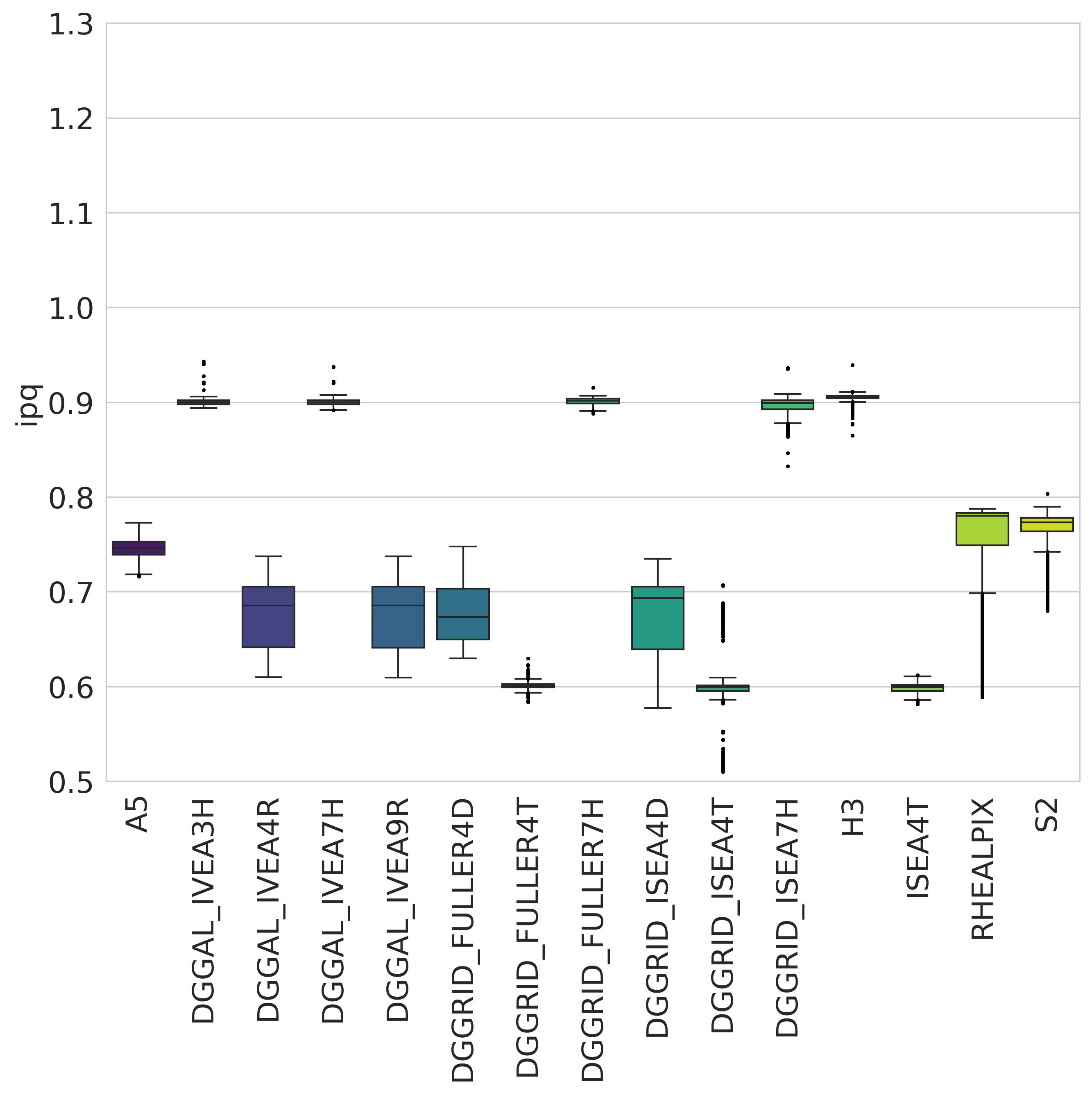
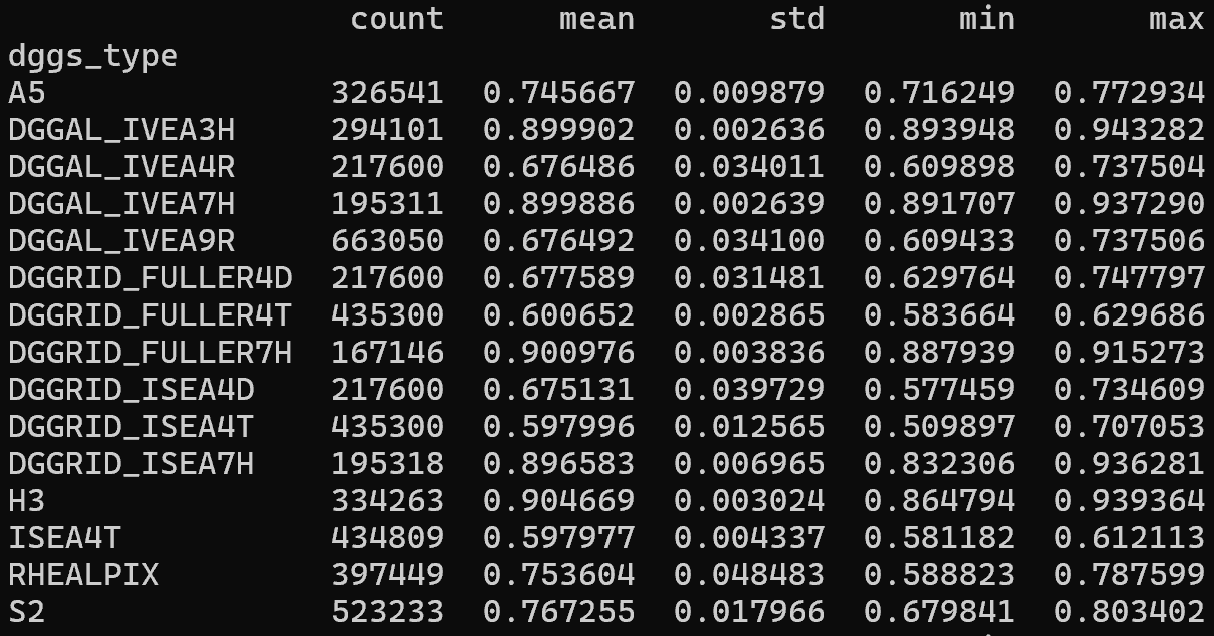
IPQ compactness distribution over popular geodesic DGGS¶

Isoperimetric Inequality (IPQ) Compactness (suggested by Osserman, 1978):

$$C_{IPQ} = \frac{4 \pi A}{p^2}$$

The range of the IPQ compactness metric is [0,1].

A circle represents the maximum compactness with a value of 1.

As shapes become more irregular or elongated, their compactness decreases toward 0.

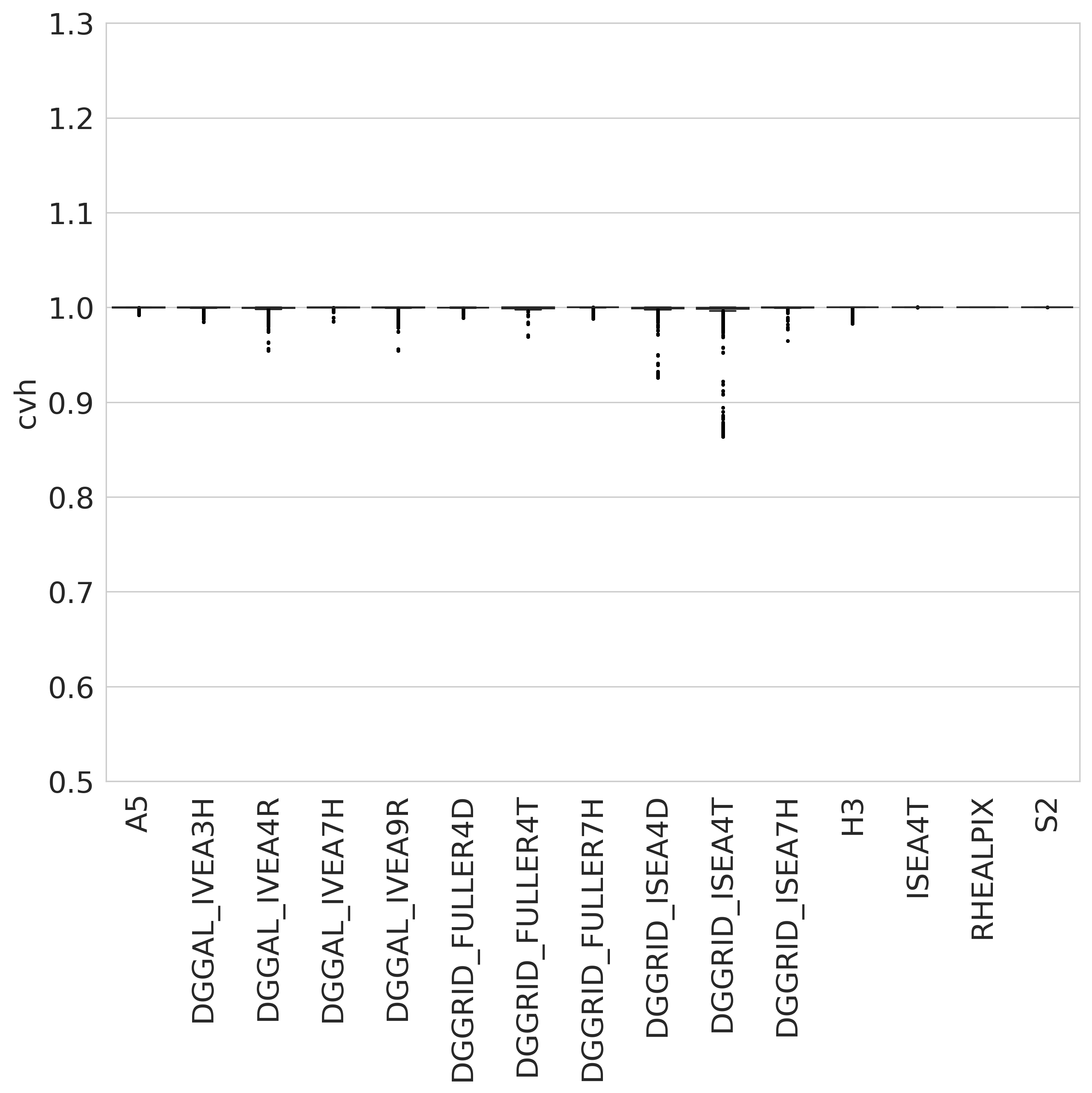
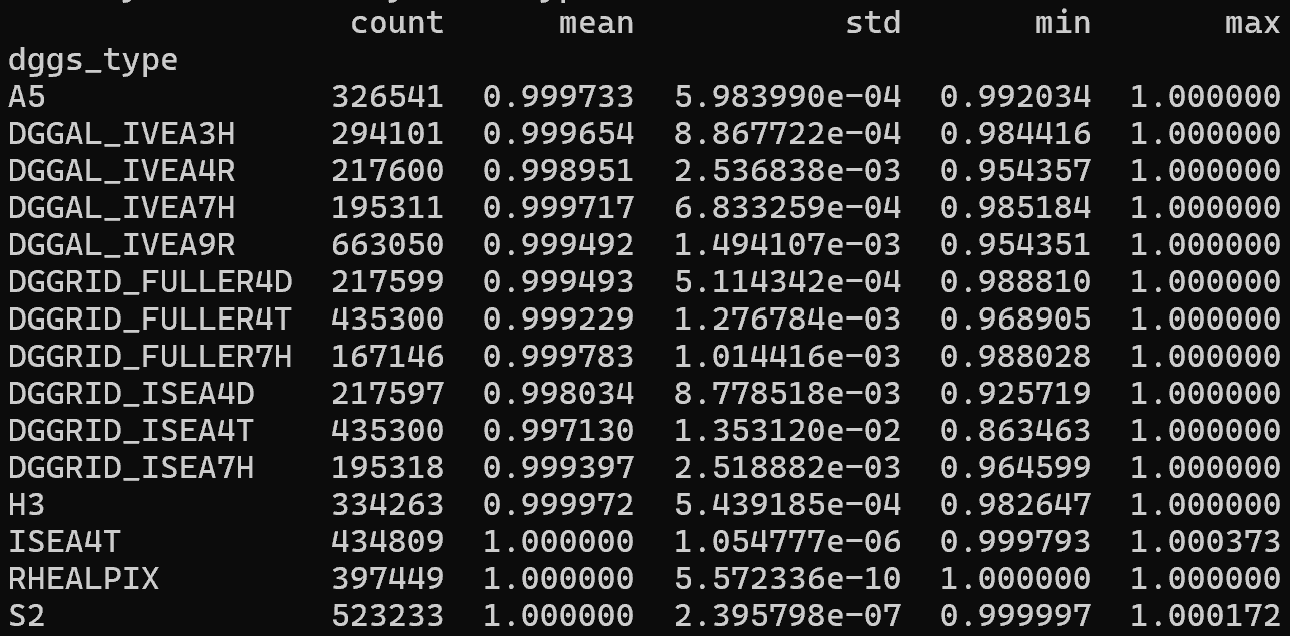
Convex hull compactness distribution over popular geodesic DGGS¶

$$C_{CVH} = \frac{A}{A_{CVH}}$$

The range of the convex hull compactness metric is [0,1].

As shapes become more concave, their convex hull compactness decreases toward 0.

Install vgrid¶

Uncomment the following line to install vgrid.

In [1]:

# %pip install vgrid --upgrade

# %pip install vgrid --upgrade

DGGS Statistics (H3 as an example, the same function pattern for other DGGSs)¶

Characteristic Length Scale (CLS - suggested by Ralph Kahn): the diameter of a spherical cap of the same cell's area

In [16]:

from vgrid.stats.h3stats import h3stats
h3_stats = h3stats("m")
h3_stats

from vgrid.stats.h3stats import h3stats h3_stats = h3stats("m") h3_stats

Out[16]:

	resolution	number_of_cells	avg_edge_len_m	avg_area_m	min_area_m	max_area_m	max_min_ratio	cls_m
0	0	122	1.281256e+06	4.357449e+12	2.562182e+12	4.977807e+12	1.942800	2.358802e+06
1	1	842	4.830568e+05	6.097884e+11	3.284346e+11	7.294869e+11	2.221102	8.813151e+05
2	2	5882	1.825130e+05	8.680178e+10	4.493090e+10	1.045998e+11	2.328015	3.324541e+05
3	3	41162	6.897922e+04	1.239343e+10	6.315472e+09	1.495077e+10	2.367325	1.256182e+05
4	4	288122	2.607176e+04	1.770348e+09	8.965824e+08	2.135987e+09	2.382366	4.747714e+04
5	5	2016842	9.854091e+03	2.529039e+08	1.277856e+08	3.051443e+08	2.387940	1.794456e+04
6	6	14117882	3.724533e+03	3.612906e+07	1.823875e+07	4.359211e+07	2.390082	6.782400e+03
7	7	98825162	1.406476e+03	5.161293e+06	2.604669e+06	6.227446e+06	2.390878	2.563506e+03
8	8	691776122	5.314140e+02	7.373276e+05	3.720480e+05	8.896352e+05	2.391184	9.689142e+02
9	9	4842432842	2.007861e+02	1.053325e+05	5.314719e+04	1.270907e+05	2.391297	3.662151e+02
10	10	33897029882	7.586378e+01	1.504750e+04	7.592318e+03	1.815582e+04	2.391341	1.384163e+02
11	11	237279209162	2.866390e+01	2.149643e+03	1.084609e+03	2.593689e+03	2.391357	5.231645e+01
12	12	1660954464122	1.083019e+01	3.070919e+02	1.549438e+02	3.705269e+02	2.391363	1.977376e+01
13	13	11626681248842	4.092010e+00	4.387027e+01	2.213481e+01	5.293242e+01	2.391366	7.473778e+00
14	14	81386768741882	1.546100e+00	6.267181e+00	3.162114e+00	7.561774e+00	2.391367	2.824823e+00
15	15	569707381193162	5.841690e-01	8.953116e-01	4.517305e-01	1.080253e+00	2.391367	1.067683e+00

DGGS Inspect¶

In [3]:

from vgrid.stats.h3stats import h3inspect

resolution = 3
h3_inspect = h3inspect(resolution)
h3_inspect = h3_inspect[
    ~h3_inspect["crossed"]
]  # remove cells that cross the Antimeridian
h3_inspect.head()

from vgrid.stats.h3stats import h3inspect resolution = 3 h3_inspect = h3inspect(resolution) h3_inspect = h3_inspect[ ~h3_inspect["crossed"] ] # remove cells that cross the Antimeridian h3_inspect.head()

Generating H3 DGGS: 100%|██████████| 41162/41162 [00:03<00:00, 13370.02 cells/s]

Out[3]:

	h3	resolution	center_lat	center_lon	avg_edge_len	cell_area	cell_perimeter	geometry	crossed	is_pentagon	norm_area	ipq	zsc	cvh
0	830000fffffffff	3	79.243774	38.024416	68843.990170	1.229263e+10	413063.941020	POLYGON ((38.40265 78.62862, 40.9926 78.94864,...	False	False	0.992008	0.905357	0.951491	1.0
1	830001fffffffff	3	80.118133	34.269779	68959.671785	1.233470e+10	413758.030713	POLYGON ((34.90645 79.50578, 37.59652 79.85885...	False	False	0.995403	0.905410	0.951519	1.0
2	830002fffffffff	3	79.248915	43.752678	69357.427250	1.247975e+10	416144.563503	POLYGON ((43.80951 78.62667, 46.57082 78.89905...	False	False	1.007109	0.905581	0.951609	1.0
3	830003fffffffff	3	80.192303	40.496153	69494.752859	1.253001e+10	416968.517157	POLYGON ((40.75903 79.56831, 43.68502 79.87171...	False	False	1.011165	0.905638	0.951639	1.0
4	830004fffffffff	3	78.291383	35.976646	68171.344007	1.204928e+10	409028.064042	POLYGON ((36.42872 77.68575, 38.74177 78.01773...	False	False	0.972370	0.905034	0.951321	1.0

DGGS Normalized Area Histogram¶

In [4]:

from vgrid.stats.h3stats import h3_norm_area_hist

h3_norm_area_hist(h3_inspect)

from vgrid.stats.h3stats import h3_norm_area_hist h3_norm_area_hist(h3_inspect)

Distribution of DGGS Area Distortions¶

In [5]:

from vgrid.stats.h3stats import h3_norm_area

h3_norm_area(h3_inspect)

from vgrid.stats.h3stats import h3_norm_area h3_norm_area(h3_inspect)

DGGS IPQ Compactness Histogram¶

In [6]:

from vgrid.stats.h3stats import h3_compactness_ipq_hist

h3_compactness_ipq_hist(h3_inspect)

from vgrid.stats.h3stats import h3_compactness_ipq_hist h3_compactness_ipq_hist(h3_inspect)

Distribution of DGGS IPQ Compactness¶

In [7]:

from vgrid.stats.h3stats import h3_compactness_ipq

h3_compactness_ipq(h3_inspect)

from vgrid.stats.h3stats import h3_compactness_ipq h3_compactness_ipq(h3_inspect)

DGGS Convex hull Compactness Histogram¶

In [8]:

from vgrid.stats.h3stats import h3_compactness_cvh_hist

h3_compactness_cvh_hist(h3_inspect)

from vgrid.stats.h3stats import h3_compactness_cvh_hist h3_compactness_cvh_hist(h3_inspect)

Distribution of DGGS Convex hull Compactness¶

In [9]:

from vgrid.stats.h3stats import h3_compactness_cvh

h3_compactness_cvh(h3_inspect)

from vgrid.stats.h3stats import h3_compactness_cvh h3_compactness_cvh(h3_inspect)

Polyhedra Generator¶

Tetrahedron¶

In [10]:

from vgrid.generator.polyhedra import tetrahedron

tetrahedron_gdf = tetrahedron()
tetrahedron_gdf.plot(edgecolor="white")

from vgrid.generator.polyhedra import tetrahedron tetrahedron_gdf = tetrahedron() tetrahedron_gdf.plot(edgecolor="white")

Out[10]:

<Axes: >

Cube¶

In [11]:

from vgrid.generator.polyhedra import cube

cube_gdf = cube()
cube_gdf.plot(edgecolor="white")

from vgrid.generator.polyhedra import cube cube_gdf = cube() cube_gdf.plot(edgecolor="white")

Generating DGGS: 100%|██████████| 6/6 [00:00<00:00, 2987.75 cells/s]

Out[11]:

<Axes: >

Octahedron¶

In [12]:

from vgrid.generator.polyhedra import octahedron

octa_gdf = octahedron()
octa_gdf.plot(edgecolor="white")

from vgrid.generator.polyhedra import octahedron octa_gdf = octahedron() octa_gdf.plot(edgecolor="white")

Out[12]:

<Axes: >

Dodecahedron¶

In [13]:

from vgrid.generator.polyhedra.dodecahedron import dodecahedron

dodecahedron_gdf = dodecahedron()
dodecahedron_gdf.plot(edgecolor="white")

from vgrid.generator.polyhedra.dodecahedron import dodecahedron dodecahedron_gdf = dodecahedron() dodecahedron_gdf.plot(edgecolor="white")

Generating dodecahedron: 100%|██████████| 12/12 [00:00<00:00, 557.74it/s]

Out[13]:

<Axes: >

Fuller Icosahedron¶

In [14]:

from vgrid.generator.polyhedra import fuller_icosahedron

fuller_icosahedron_gdf = fuller_icosahedron()
fuller_icosahedron_gdf.plot()
fuller_icosahedron_gdf.to_file("fuller_icosahedron.geojson")

from vgrid.generator.polyhedra import fuller_icosahedron fuller_icosahedron_gdf = fuller_icosahedron() fuller_icosahedron_gdf.plot() fuller_icosahedron_gdf.to_file("fuller_icosahedron.geojson")

Rhombic Icosahedron¶

In [15]:

from vgrid.generator.polyhedra import rhombic_icosahedron

rhombic_icosahedron_gdf = rhombic_icosahedron()
rhombic_icosahedron_gdf.plot(edgecolor="white")

from vgrid.generator.polyhedra import rhombic_icosahedron rhombic_icosahedron_gdf = rhombic_icosahedron() rhombic_icosahedron_gdf.plot(edgecolor="white")

Generating Rhombic Icosahedron: 100%|██████████| 10/10 [00:00<00:00, 500.01it/s]

Out[15]:

<Axes: >